数据结构&算法实践—【排序|选择排序】堆排序

排序»选择排序»堆排序

List:

0.概念+伪代码+示例分析
1.堆排序实现
2.Question

0. start

基本概念：

维基百科http://zh.wikipedia.org/zh-cn/%E5%A0%86%E7%A9%8D%E6%8E%92%E5%BA%8F

function heapSort(A : list[1..n]) {
    max_heap = make_max_heap(A)  #构建一个最大堆
    i = 1
    while(max_heap.size() > 0){   #当堆中还存在值
        A[n-i] = max_heap.pop_max()   #取出最大一个
        i++
    }
}

堆为一棵完全二叉树，每个节点值都>=子节点值

堆排序根据这个特性，首先将所有元素建立堆，然后一个个取出，即有序的

堆中每个节点的位置：

父节点i的左子节点在位置 (2*i);
父节点i的右子节点在位置 (2*i+1);
子节点i的父节点在位置 floor(i/2);

最大堆主要操作逻辑：

插入：将新元素加入完全二叉树最后一个节点，依次往上，调整直到满足父节点值都>=子节点值

删除：移除根节点，将最后一个节点拿到根节点，依次往下，调整

原始:

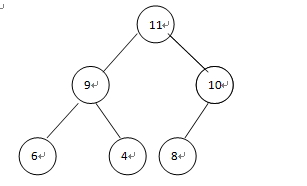
插入操作：12，先假定放在最后一个位置，然后从这个节点开始往上，同父节点比较，依次调整

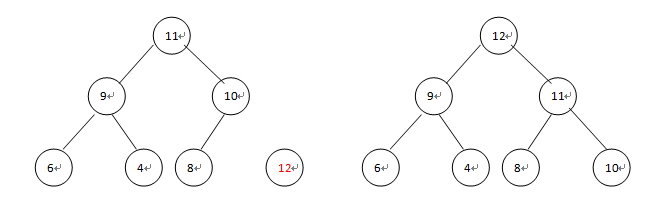
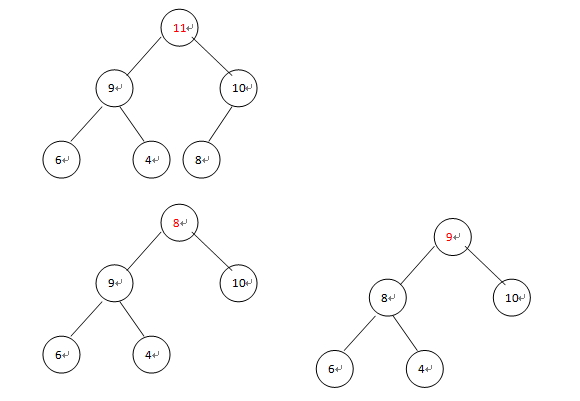
删除：取走11，将最后一个元素8移到根节点，从上往下，重新调整

1. start

根据公式，我们可以使用数组模拟实现完全二叉树(不使用首个位置)

首先，我们先实现堆:

#!/usr/bin/python
# -*- coding:utf-8 -*-
#堆排序
#@author: wklken@yeah.net

#先实现一个最大堆
class MaxHeap:
    def __init__(self):
        self.heap = [0]  #第一个元素用不到，只是为了将下标转为1开始，方便计算节点的位置
    def isEmpty(self):
        return len(self.heap) == 1
    def size(self):
        return len(self.heap) - 1
    #插入节点
    def insert(self, value):
        i = len(self.heap)
        self.heap.append(value)
        while i != 1 and value > self.heap[i/2]:  #如果插入节点大于其父节点，需要交换二者,反复，直到值小于父节点
            self.heap[i], self.heap[i/2] = self.heap[i/2], self.heap[i]  #父节点下移
            i = i/2
        self.heap[i] = value  #把 value插入对应位置
    #删除最大节点——最大的是根节点
    def deleteMax(self):
        if self.isEmpty(): #没有元素了
            return None
        x = self.heap[1]  #最大

        last = self.heap.pop()
        if self.size() == 0: #每次取最后一个，若是只剩两个的情况，pop
            return x
        #每次，移除根节点，将树的最后一个节点挪到根节点，然后从上到下，调整位置，保证树是一个最大堆
        i = 1
        ci = 2
        current_size = self.size()
        while  ci <= current_size:
            if ci < current_size and self.heap[ci] < self.heap[ci+1]:
                ci += 1

            if last >= self.heap[ci]:
                break

            self.heap[i] = self.heap[ci]
            i = ci
            ci *= 2
        self.heap[i] = last
        return x

    def initFromList(self, l):
        self.heap.extend(l)
        size = self.size()
        #从最后一棵子树开始，调整每一棵子树
        for i in range(size/2,0,-1):
              t_root = self.heap[i]

              c = 2*i
              while c <= size:
                  if c < size and self.heap[c] < self.heap[c+1]:
                      c += 1
                  if t_root >= self.heap[c]:
                      break
                  self.heap[c/2] = self.heap[c]
                  c *= 2
                  self.heap[c/2] = t_root

然后，实现排序过程：

:::python
def heap_sort(l):
    m = MaxHeap()
    m.initFromList(l)
    result = []
    for i in range(len(l)):
        result.append(m.deleteMax())
        print result
    return result

2. start

A.概念，过程描述？

B. 时间复杂度？空间复杂度？是否是稳定排序？

C.适用场景，何种情况下表现最优